Numerical stability
Using log-probabilities can make an algorithm more numerically stable, particularly when that algorithm involves the product of several probabilities. Multiplying probabilities together can lead to floating point overflow, resulting in a value of 0 or Inf. The sum of the logs is more resilient to this problem, since it enables the representation of much larger (and much smaller) numbers. For example:
prod(1:1000)
## [1] Inf
sum(log(1:1000))
## [1] 5912
prod(1/(1:1000))
## [1] 0
sum(log(1/(1:1000)))
## [1] -5912
Converting the product into a sum of logs should also lead to a slight speedup, although as I’ve previously noted it actually makes my code slower. I’ve resurrected my log-probability code from my Git stash and run some experiments to determine what I gain, as well as measuring the computational cost. Details after the jump.
I don’t have the exact distribution of runtimes from the old code (without sums of logs), but suffice to say I was able to reliably perform 100K iterations of pseudolikelihood in less than 24 hours. This is important, because jobs that run in under 24 hours have their own queue on the supercomputer. Thus, the longer runtime is compounded by the fact that the jobs wait for longer in the queue.
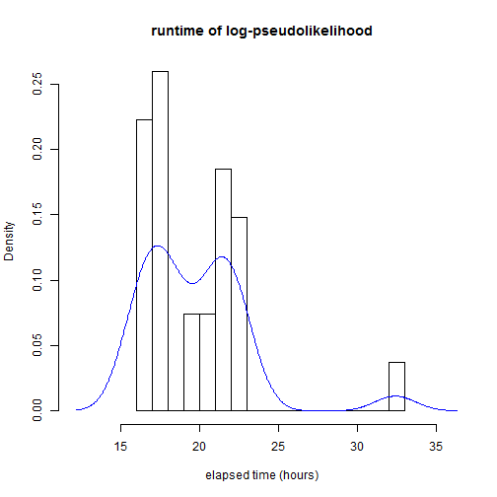
This is what the distribution of runtimes looks like for 100K iterations of log-pseudolikelihood:
load("data/results_20130417.rda") # result.pseudo from previous run
hist(as.double(result.pseudo$elapsed), main = "runtime of log-pseudolikelihood",
xlab = "elapsed time (hours)", breaks = 12, prob = T, xlim = c(12, 36))
lines(density(as.double(result.pseudo$elapsed)), col = "blue")
6 of the PBS jobs exceeded the 24 hour time limit and had to be rerun using the long queue.
=>> PBS: job killed: walltime 86458 exceeded limit 86400
Those resubmitted jobs then spent various amounts of time waiting in the queue, from 1.44 up to 8.35 hours.
This is also a handy trick, particularly for simulating from mixture distributions using the log-likelihood:
http://jblevins.org/log/log-sum-exp